diff options
Diffstat (limited to 'tensorflow/docs_src/guide/tensorboard_histograms.md')
| -rw-r--r-- | tensorflow/docs_src/guide/tensorboard_histograms.md | 245 |
1 files changed, 0 insertions, 245 deletions
diff --git a/tensorflow/docs_src/guide/tensorboard_histograms.md b/tensorflow/docs_src/guide/tensorboard_histograms.md deleted file mode 100644 index af8f2cadd1..0000000000 --- a/tensorflow/docs_src/guide/tensorboard_histograms.md +++ /dev/null @@ -1,245 +0,0 @@ -# TensorBoard Histogram Dashboard - -The TensorBoard Histogram Dashboard displays how the distribution of some -`Tensor` in your TensorFlow graph has changed over time. It does this by showing -many histograms visualizations of your tensor at different points in time. - -## A Basic Example - -Let's start with a simple case: a normally-distributed variable, where the mean -shifts over time. -TensorFlow has an op -[`tf.random_normal`](https://www.tensorflow.org/api_docs/python/tf/random_normal) -which is perfect for this purpose. As is usually the case with TensorBoard, we -will ingest data using a summary op; in this case, -['tf.summary.histogram'](https://www.tensorflow.org/api_docs/python/tf/summary/histogram). -For a primer on how summaries work, please see the -[TensorBoard guide](./summaries_and_tensorboard.md). - -Here is a code snippet that will generate some histogram summaries containing -normally distributed data, where the mean of the distribution increases over -time. - -```python -import tensorflow as tf - -k = tf.placeholder(tf.float32) - -# Make a normal distribution, with a shifting mean -mean_moving_normal = tf.random_normal(shape=[1000], mean=(5*k), stddev=1) -# Record that distribution into a histogram summary -tf.summary.histogram("normal/moving_mean", mean_moving_normal) - -# Setup a session and summary writer -sess = tf.Session() -writer = tf.summary.FileWriter("/tmp/histogram_example") - -summaries = tf.summary.merge_all() - -# Setup a loop and write the summaries to disk -N = 400 -for step in range(N): - k_val = step/float(N) - summ = sess.run(summaries, feed_dict={k: k_val}) - writer.add_summary(summ, global_step=step) -``` - -Once that code runs, we can load the data into TensorBoard via the command line: - - -```sh -tensorboard --logdir=/tmp/histogram_example -``` - -Once TensorBoard is running, load it in Chrome or Firefox and navigate to the -Histogram Dashboard. Then we can see a histogram visualization for our normally -distributed data. - -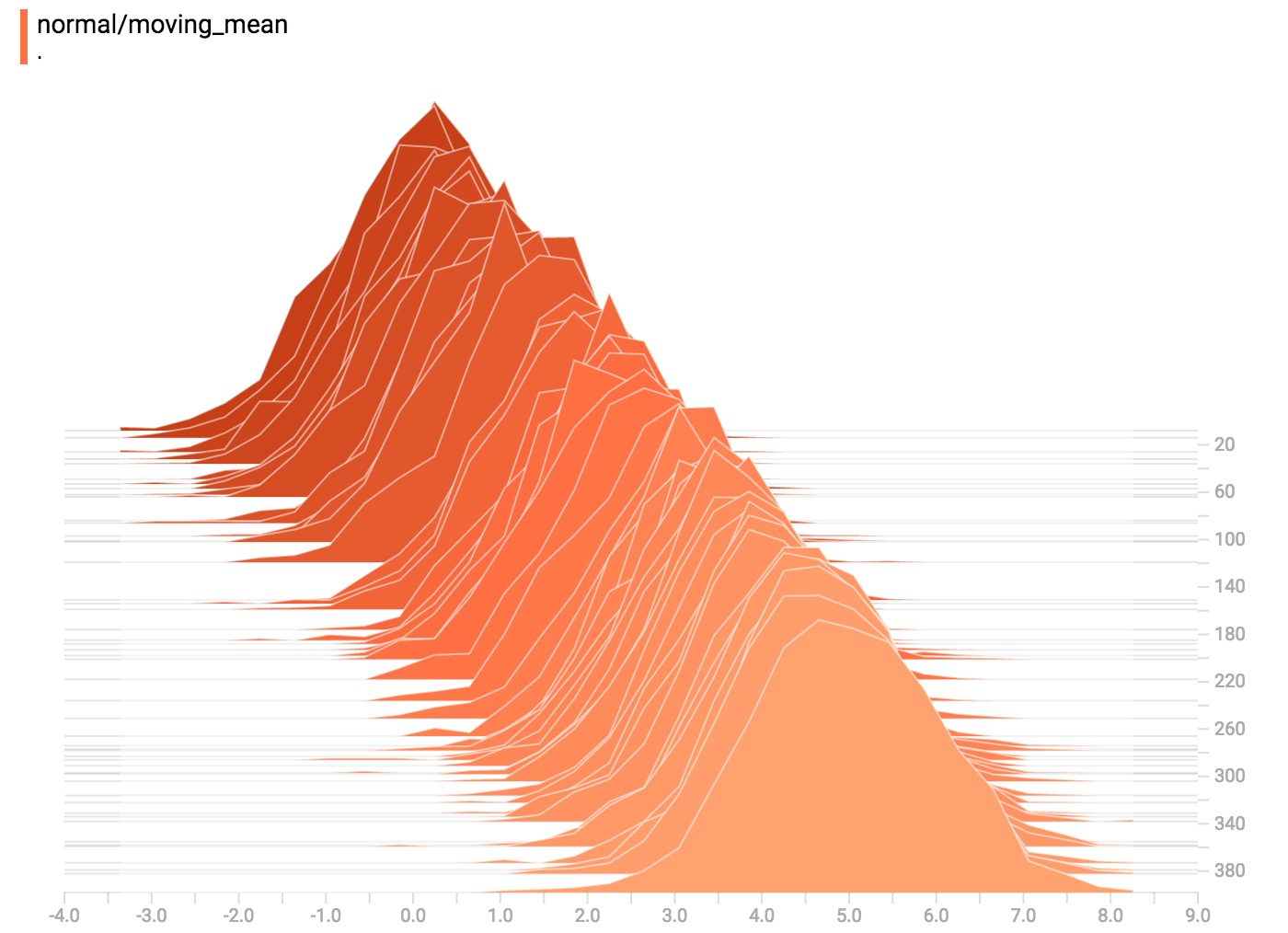 - -`tf.summary.histogram` takes an arbitrarily sized and shaped Tensor, and -compresses it into a histogram data structure consisting of many bins with -widths and counts. For example, let's say we want to organize the numbers -`[0.5, 1.1, 1.3, 2.2, 2.9, 2.99]` into bins. We could make three bins: -* a bin -containing everything from 0 to 1 (it would contain one element, 0.5), -* a bin -containing everything from 1-2 (it would contain two elements, 1.1 and 1.3), -* a bin containing everything from 2-3 (it would contain three elements: 2.2, -2.9 and 2.99). - -TensorFlow uses a similar approach to create bins, but unlike in our example, it -doesn't create integer bins. For large, sparse datasets, that might result in -many thousands of bins. -Instead, [the bins are exponentially distributed, with many bins close to 0 and -comparatively few bins for very large numbers.](https://github.com/tensorflow/tensorflow/blob/c8b59c046895fa5b6d79f73e0b5817330fcfbfc1/tensorflow/core/lib/histogram/histogram.cc#L28) -However, visualizing exponentially-distributed bins is tricky; if height is used -to encode count, then wider bins take more space, even if they have the same -number of elements. Conversely, encoding count in the area makes height -comparisons impossible. Instead, the histograms [resample the data](https://github.com/tensorflow/tensorflow/blob/17c47804b86e340203d451125a721310033710f1/tensorflow/tensorboard/components/tf_backend/backend.ts#L400) -into uniform bins. This can lead to unfortunate artifacts in some cases. - -Each slice in the histogram visualizer displays a single histogram. -The slices are organized by step; -older slices (e.g. step 0) are further "back" and darker, while newer slices -(e.g. step 400) are close to the foreground, and lighter in color. -The y-axis on the right shows the step number. - -You can mouse over the histogram to see tooltips with some more detailed -information. For example, in the following image we can see that the histogram -at timestep 176 has a bin centered at 2.25 with 177 elements in that bin. - -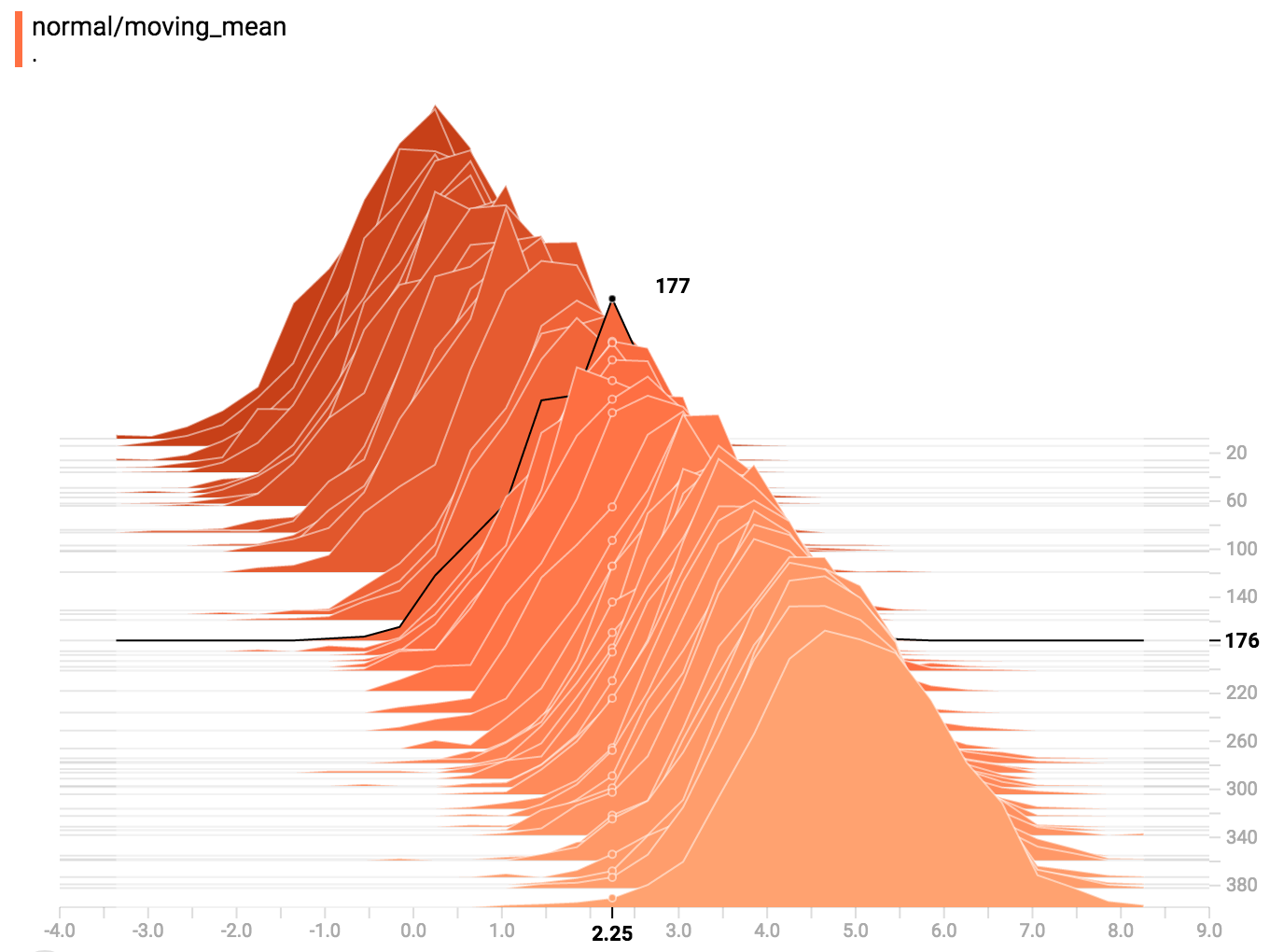 - -Also, you may note that the histogram slices are not always evenly spaced in -step count or time. This is because TensorBoard uses -[reservoir sampling](https://en.wikipedia.org/wiki/Reservoir_sampling) to keep a -subset of all the histograms, to save on memory. Reservoir sampling guarantees -that every sample has an equal likelihood of being included, but because it is -a randomized algorithm, the samples chosen don't occur at even steps. - -## Overlay Mode - -There is a control on the left of the dashboard that allows you to toggle the -histogram mode from "offset" to "overlay": - -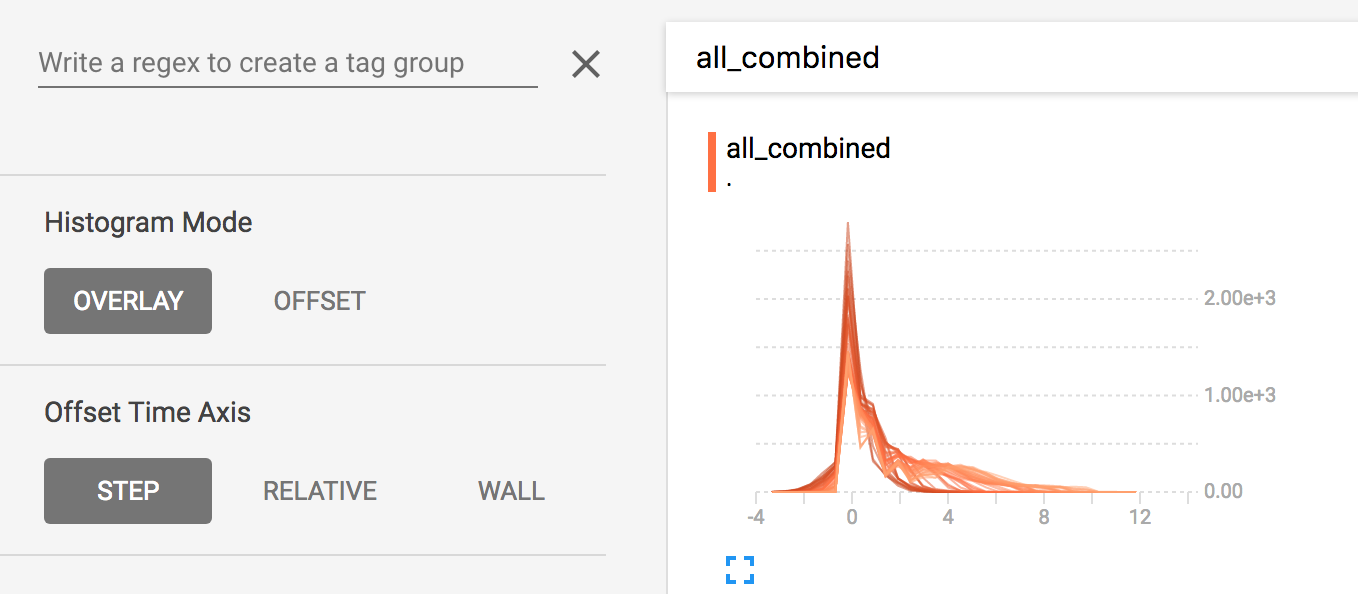 - -In "offset" mode, the visualization rotates 45 degrees, so that the individual -histogram slices are no longer spread out in time, but instead are all plotted -on the same y-axis. - -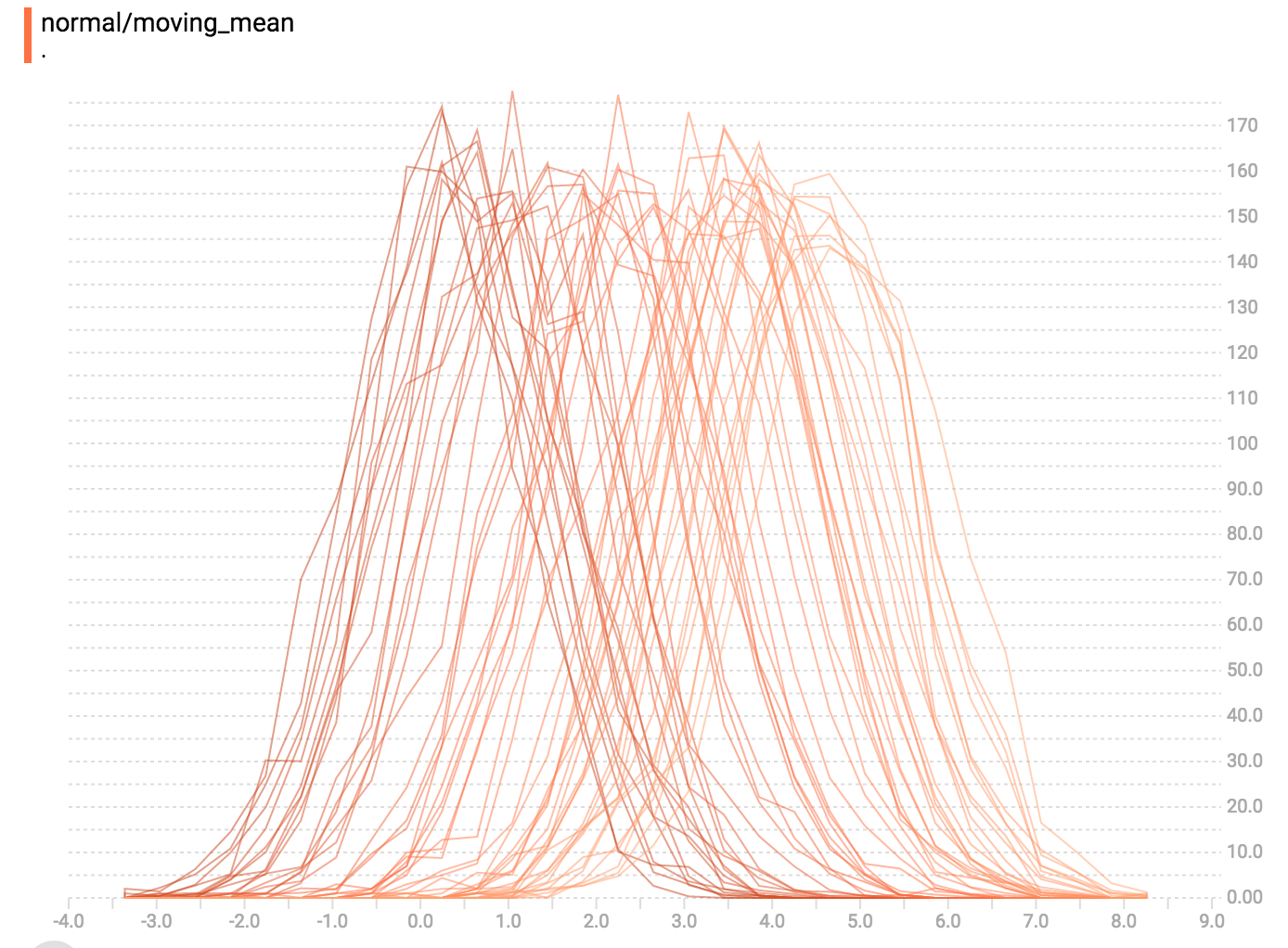 -Now, each slice is a separate line on the chart, and the y-axis shows the item -count within each bucket. Darker lines are older, earlier steps, and lighter -lines are more recent, later steps. Once again, you can mouse over the chart to -see some additional information. - -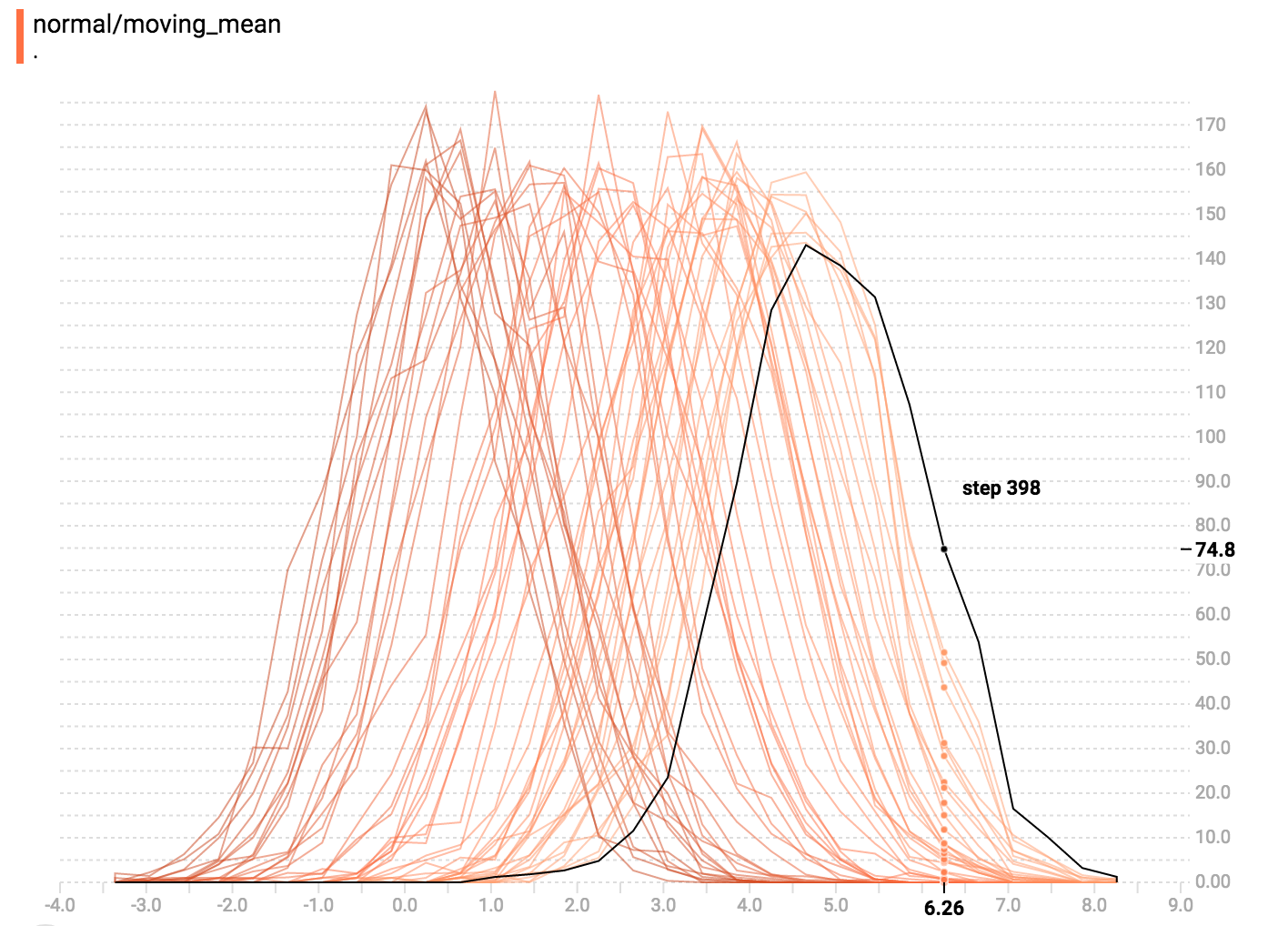 - -In general, the overlay visualization is useful if you want to directly compare -the counts of different histograms. - -## Multimodal Distributions - -The Histogram Dashboard is great for visualizing multimodal -distributions. Let's construct a simple bimodal distribution by concatenating -the outputs from two different normal distributions. The code will look like -this: - -```python -import tensorflow as tf - -k = tf.placeholder(tf.float32) - -# Make a normal distribution, with a shifting mean -mean_moving_normal = tf.random_normal(shape=[1000], mean=(5*k), stddev=1) -# Record that distribution into a histogram summary -tf.summary.histogram("normal/moving_mean", mean_moving_normal) - -# Make a normal distribution with shrinking variance -variance_shrinking_normal = tf.random_normal(shape=[1000], mean=0, stddev=1-(k)) -# Record that distribution too -tf.summary.histogram("normal/shrinking_variance", variance_shrinking_normal) - -# Let's combine both of those distributions into one dataset -normal_combined = tf.concat([mean_moving_normal, variance_shrinking_normal], 0) -# We add another histogram summary to record the combined distribution -tf.summary.histogram("normal/bimodal", normal_combined) - -summaries = tf.summary.merge_all() - -# Setup a session and summary writer -sess = tf.Session() -writer = tf.summary.FileWriter("/tmp/histogram_example") - -# Setup a loop and write the summaries to disk -N = 400 -for step in range(N): - k_val = step/float(N) - summ = sess.run(summaries, feed_dict={k: k_val}) - writer.add_summary(summ, global_step=step) -``` - -You already remember our "moving mean" normal distribution from the example -above. Now we also have a "shrinking variance" distribution. Side-by-side, they -look like this: -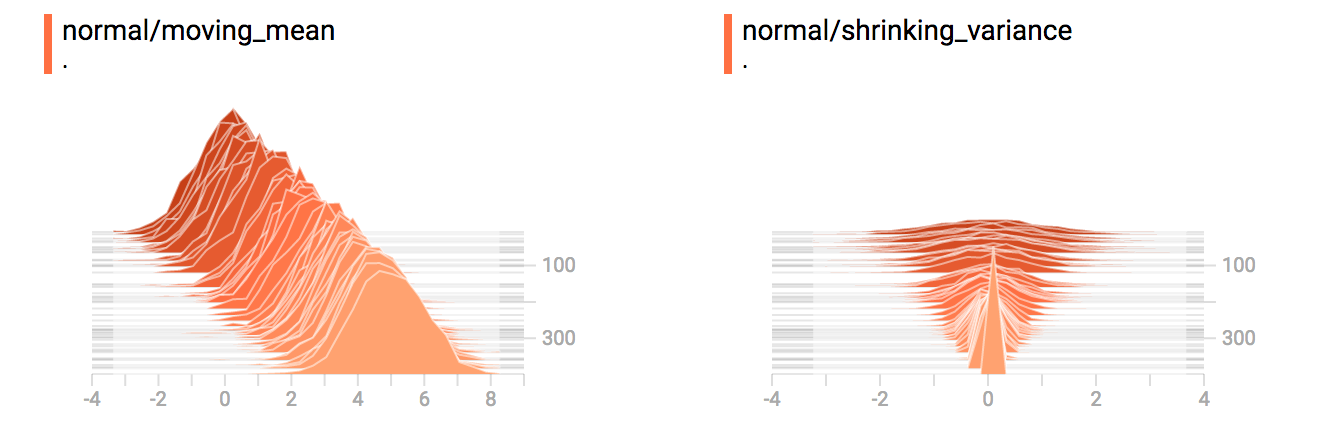 - -When we concatenate them, we get a chart that clearly reveals the divergent, -bimodal structure: -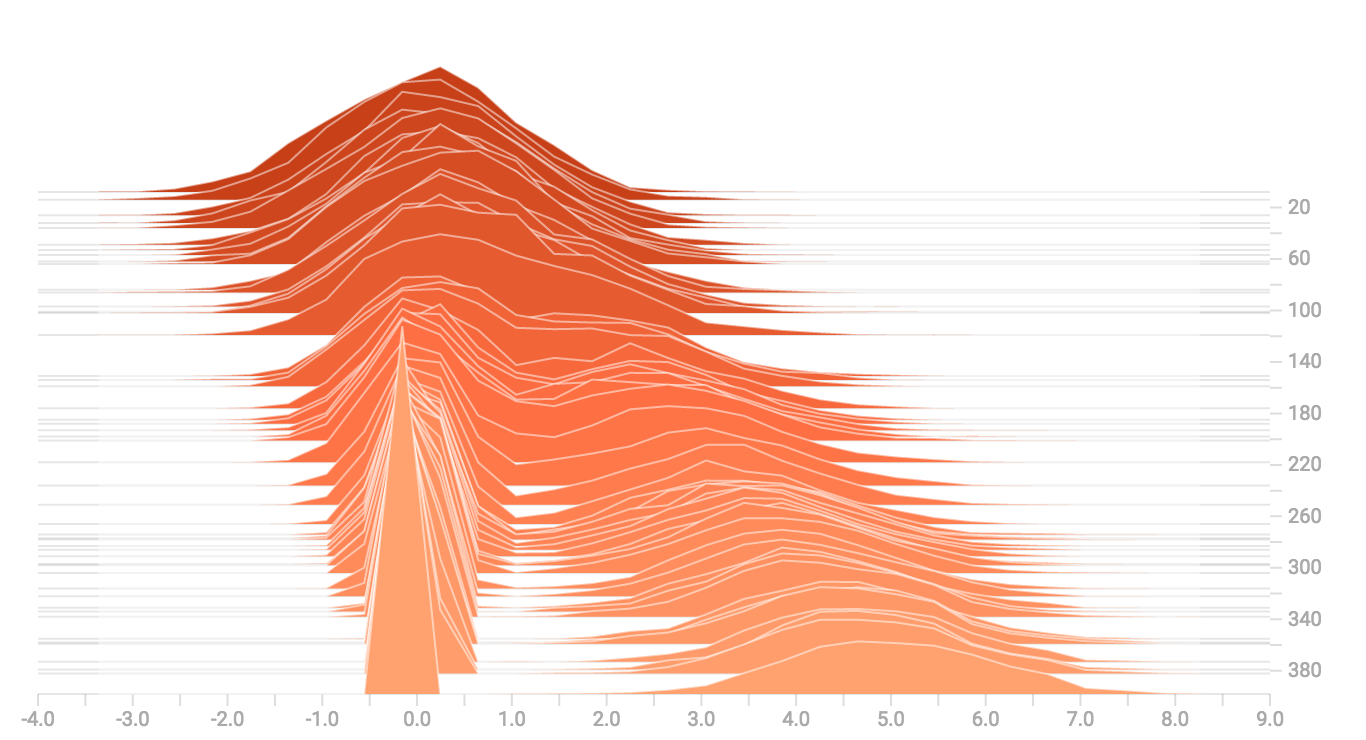 - -## Some more distributions - -Just for fun, let's generate and visualize a few more distributions, and then -combine them all into one chart. Here's the code we'll use: - -```python -import tensorflow as tf - -k = tf.placeholder(tf.float32) - -# Make a normal distribution, with a shifting mean -mean_moving_normal = tf.random_normal(shape=[1000], mean=(5*k), stddev=1) -# Record that distribution into a histogram summary -tf.summary.histogram("normal/moving_mean", mean_moving_normal) - -# Make a normal distribution with shrinking variance -variance_shrinking_normal = tf.random_normal(shape=[1000], mean=0, stddev=1-(k)) -# Record that distribution too -tf.summary.histogram("normal/shrinking_variance", variance_shrinking_normal) - -# Let's combine both of those distributions into one dataset -normal_combined = tf.concat([mean_moving_normal, variance_shrinking_normal], 0) -# We add another histogram summary to record the combined distribution -tf.summary.histogram("normal/bimodal", normal_combined) - -# Add a gamma distribution -gamma = tf.random_gamma(shape=[1000], alpha=k) -tf.summary.histogram("gamma", gamma) - -# And a poisson distribution -poisson = tf.random_poisson(shape=[1000], lam=k) -tf.summary.histogram("poisson", poisson) - -# And a uniform distribution -uniform = tf.random_uniform(shape=[1000], maxval=k*10) -tf.summary.histogram("uniform", uniform) - -# Finally, combine everything together! -all_distributions = [mean_moving_normal, variance_shrinking_normal, - gamma, poisson, uniform] -all_combined = tf.concat(all_distributions, 0) -tf.summary.histogram("all_combined", all_combined) - -summaries = tf.summary.merge_all() - -# Setup a session and summary writer -sess = tf.Session() -writer = tf.summary.FileWriter("/tmp/histogram_example") - -# Setup a loop and write the summaries to disk -N = 400 -for step in range(N): - k_val = step/float(N) - summ = sess.run(summaries, feed_dict={k: k_val}) - writer.add_summary(summ, global_step=step) -``` -### Gamma Distribution -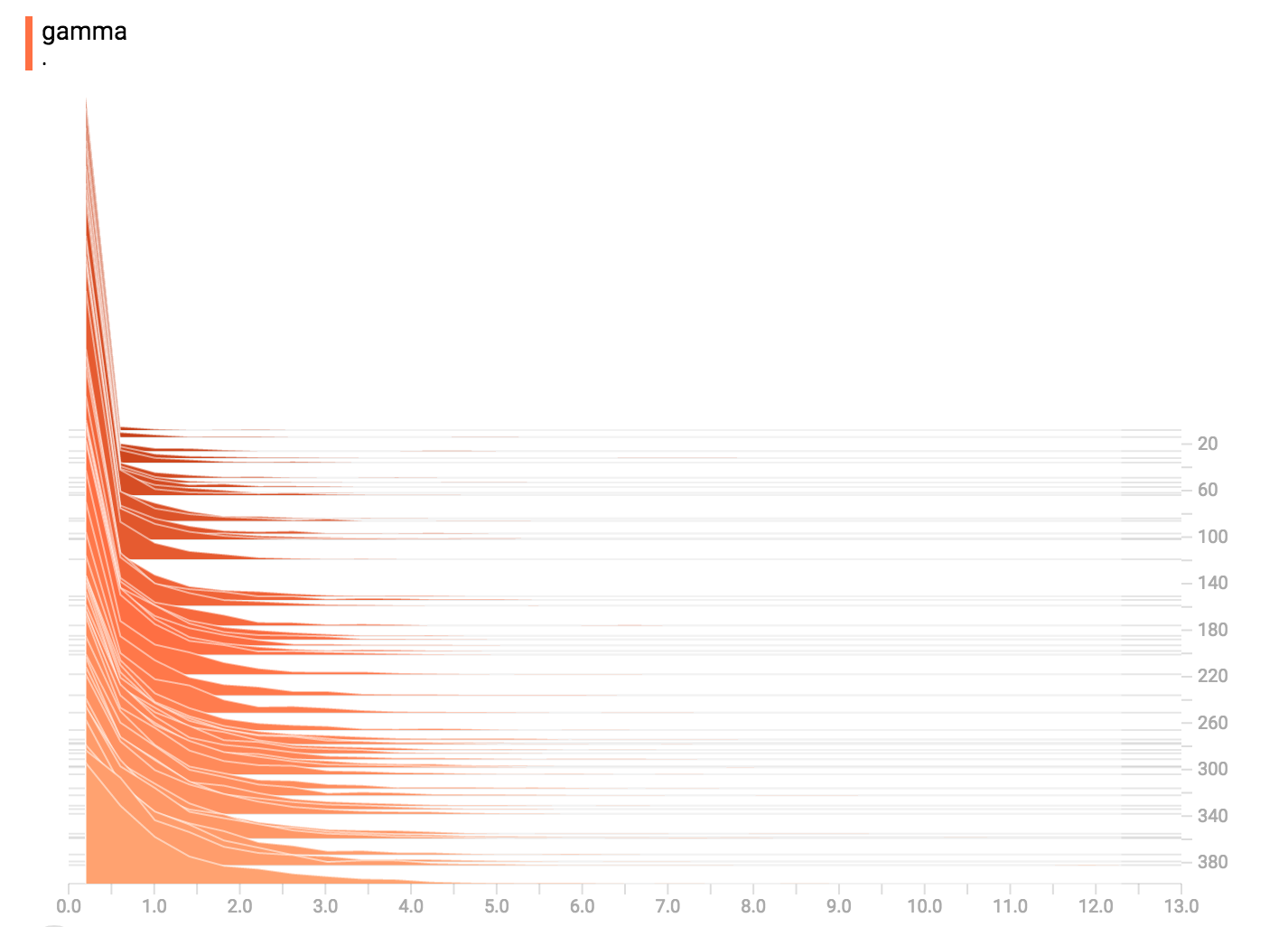 - -### Uniform Distribution -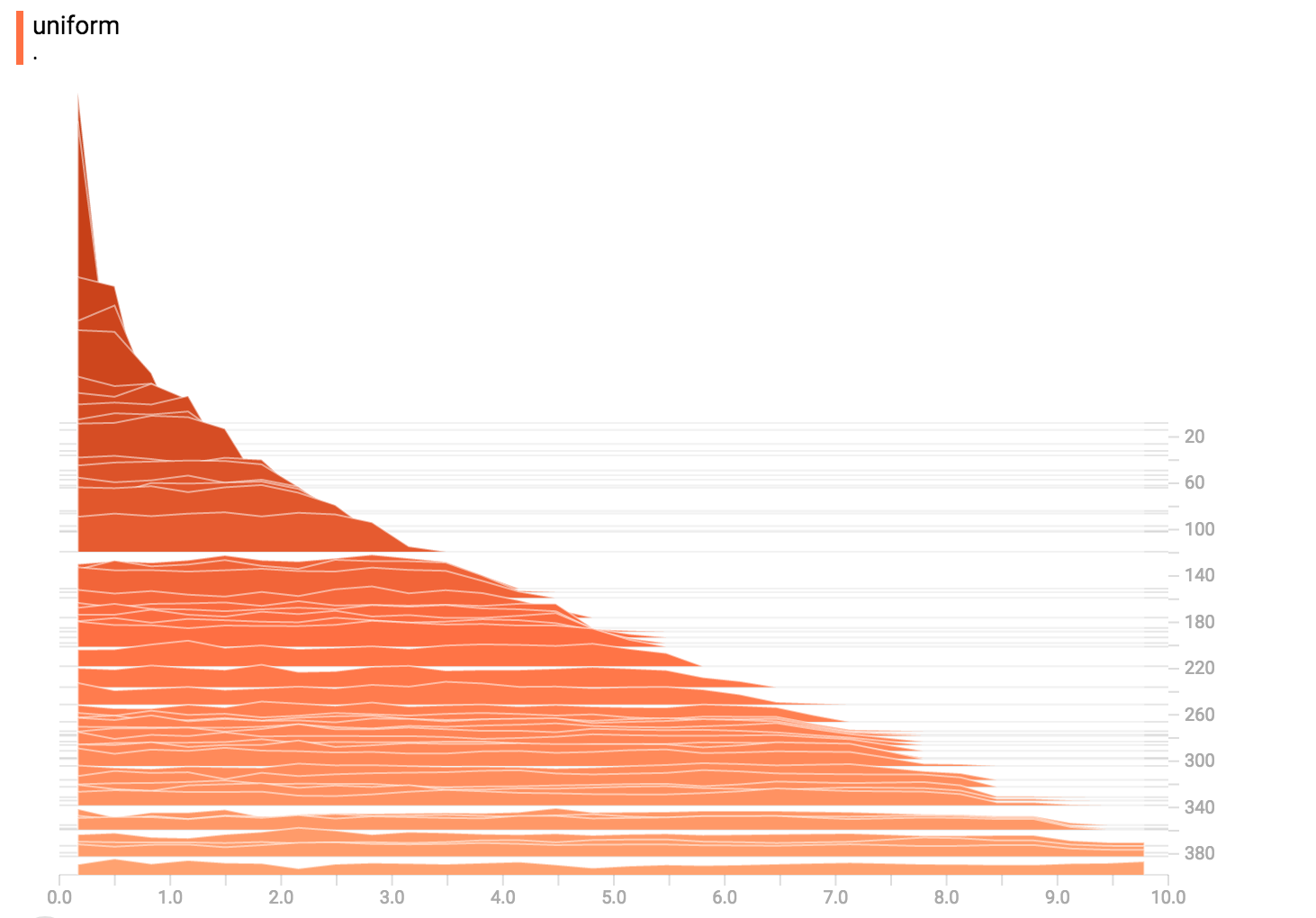 - -### Poisson Distribution -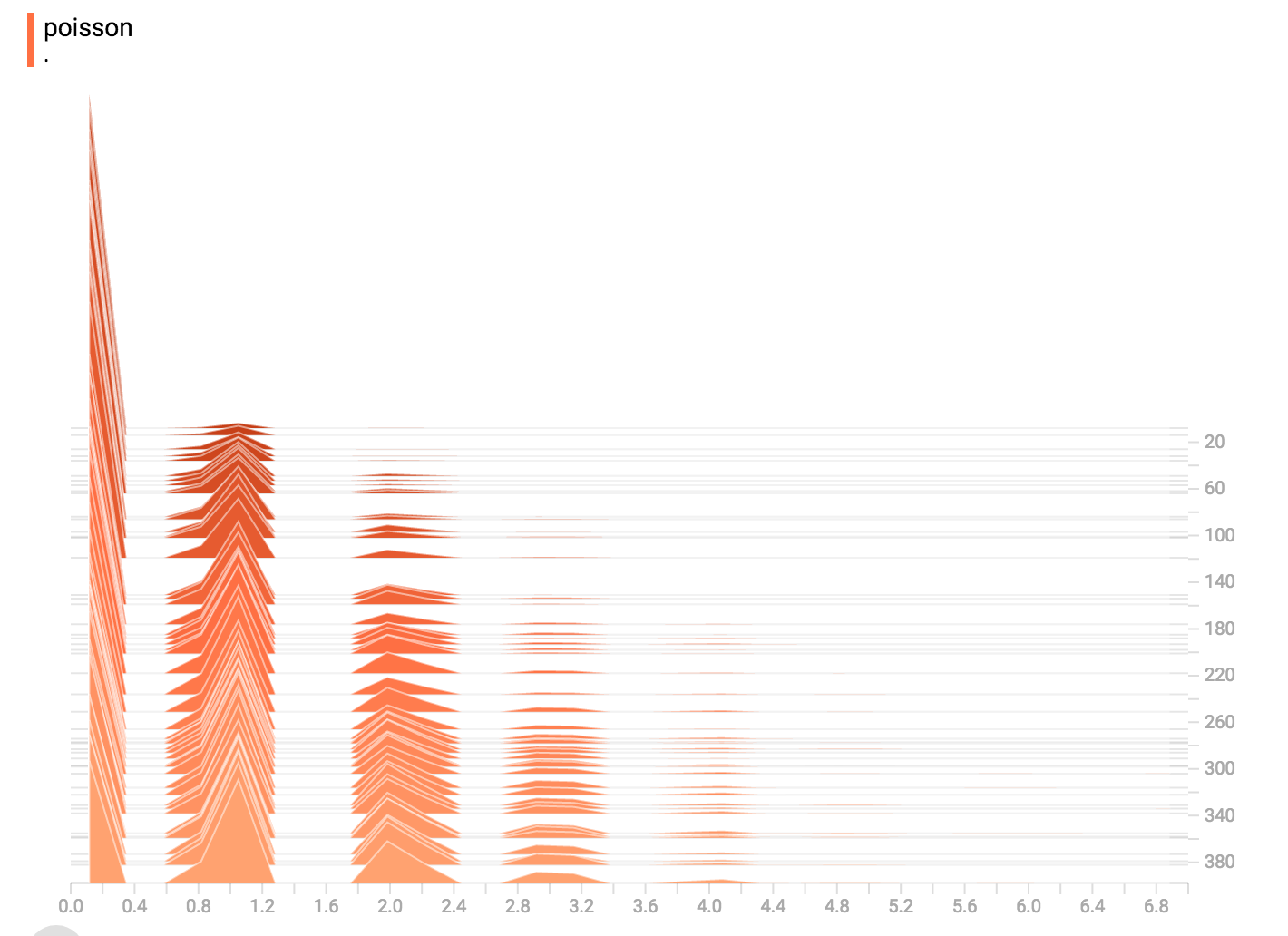 -The poisson distribution is defined over the integers. So, all of the values -being generated are perfect integers. The histogram compression moves the data -into floating-point bins, causing the visualization to show little -bumps over the integer values rather than perfect spikes. - -### All Together Now -Finally, we can concatenate all of the data into one funny-looking curve. -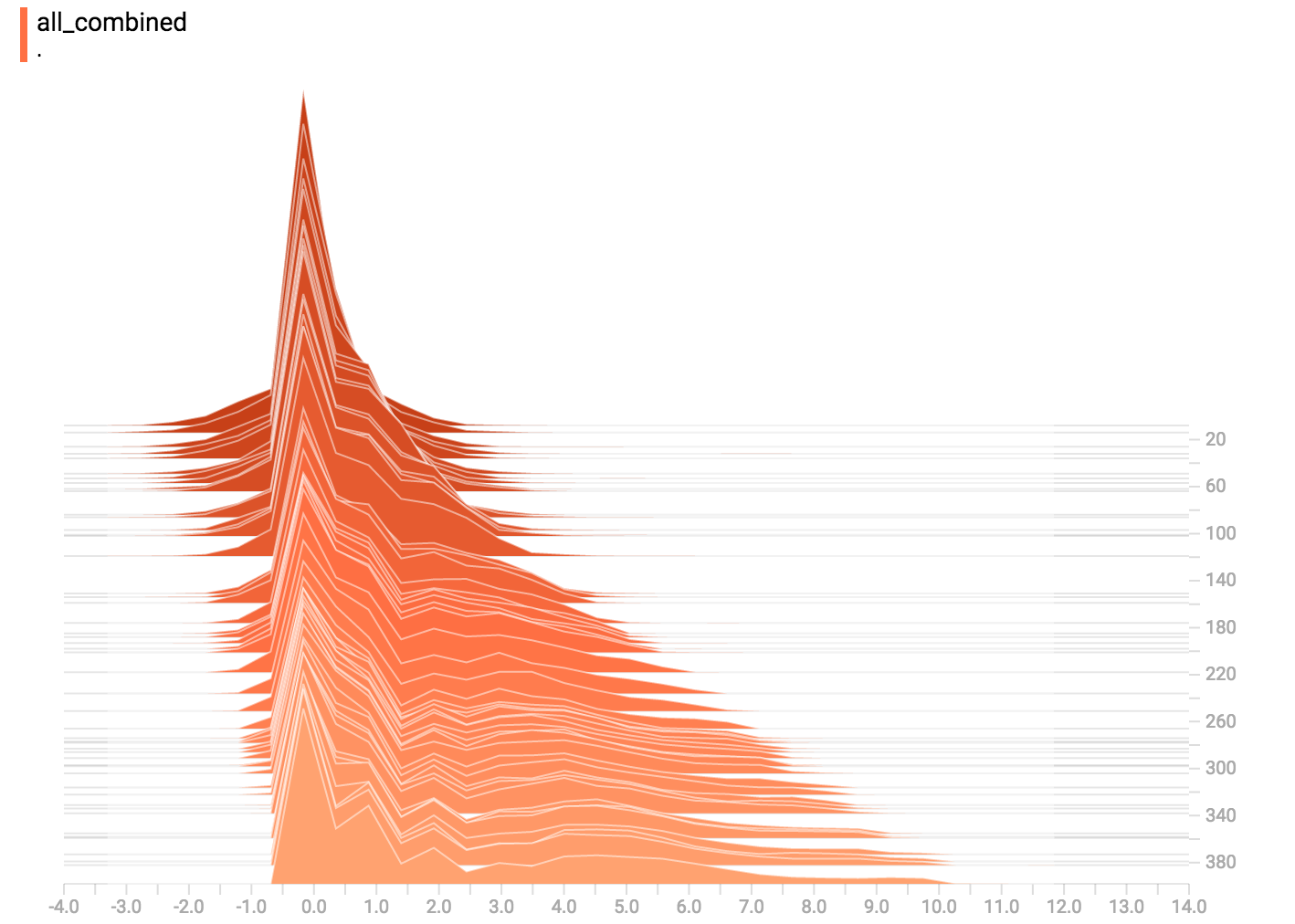 - |
